原文:A introduction to compression
译者:youngsterxyf
最近我在思考GIF和JPEG图片格式之间的不同:为什么某些图片存储为GIF格式所占的磁盘空间更大,而另一些图片以JPEG格式存储要占用更大的磁盘空间?事实证明,这是因为不同的图片格式使用了不同的压缩方法。
压缩是一组程序的简便说法,这些程序能够将数据装进更小的存储空间中,也能将数据从压缩编码中重新取回。这是一个双向的过程:输入文件能够产生经过压缩的输出,并且算法根据压缩后的输出能够重新给你一个输入的拷贝。
冗余:行程长度编码(Run-Length Encoding)
使压缩成为可能的是冗余:事实表明大多数的数据都以某种方式重复自己。例如,在一个文档中可能多次使用同一个单词,或者一张图片的多处包含相同的颜色。一个非常简单的冗余数据片段的示例如下所示:
Redundancy: Before compression
AAAAABBWWWWWWWWWPPPPQZMMMMVVV
在这种情况下,冗余是明显的;整个样本中重复出现了一系列字母。压缩这种数据的一种简单方式是通过重复次数来代表重复出现的字母,从而削减了样本的总长度。
Redundancy: After compression
A5B2W9P4Q1Z1M4V3
算法读取样本编码后的版本将能够完美地重现原来的数据:"A" 5次,"B" 2次,等等。这个简单算法的使用非常广泛,被称为行程长度编码(RLE):写下字符的每次行程有多长。以古老的PCX图像格式为例来说明一种广泛使用的标准RLE。

图1中有很多单色的实心方块。这张图片宽500个像素,高190个像素;作为一张原始位图,使用一个字节来表示一个像素,那么这张图片就产生95kB的数据。PCX算法计算图片中每行像素的行程长度,为相同颜色的连续像素保存行程长度:以这种方式,图片的大小减到了52kB。
频率:哈夫曼(Huffman)编码
RLE的一个主要问题是它处理的是数据中的连续值:图1中,RLE算法对图片的每个水平行进行独立的处理,然而其实所有的行都是相同的。这个问题可以通过整体地看待数据来缓解,构建一个表来记录在整个数据集中每个值出现的次数。
哈夫曼编码是一种借助这种“频率表”的方法,这种表记录着每个值出现的频率,并且为每一项分配一个编码。频率越高的项编码越短,较少出现的项也就得到长的编码。在计算中,这些编码一般是二进制编码,然后就可以组合成字节进行文件存储。
使用上面的例子,一个哈夫曼编码的过程如下所示:
Huffman encoding: Before compression
AAAAABBWWWWWWWWWPPPPQZMMMMVVV
| 值 | 频率 | 编码 |
|---|---|---|
| Q | 1 | 000000 |
| Z | 1 | 000001 |
| B | 2 | 00001 |
| V | 3 | 0001 |
| P | 4 | 001 |
| M | 4 | 011 |
| A | 5 | 01 |
| W | 9 | 1 |
Huffman encoding: After compression
01 01 01 01 01 00001 00001 1 1 1 1 1 1 1 1 1 001 001 001 001 000000 000001 011 011 011 011 0001 0001 0001
此处省略了一行乱码,避免atom和rss报错...
使用哈夫曼编码,数据从29个字符减少到10个字节。当然这没包含频率与编码表,这个表必须和压缩后的数据一起存储才有意义;本例中,频率表比压缩后的数据还要大,但在多数情况下,频率表的大小是微不足道的。
当然,将RLE和哈夫曼编码结合使用是可能的,首先执行RLE,然后将压缩后的结果交给哈夫曼算法处理。对于简单的图片,这会产生特别好的结果:上面的图1通过使用GIF文件格式可以从一个95kB的位图压缩成一个4kB的文件,GIF文件格式就是结合使用了RLE,哈夫曼编码以及其他算法。
感知:有损编码
上述方法可以用于以一种能够完美重现的方式对数据进行压缩。这种压缩的用例包括文档和软件程序,对于这种用例来说,任意值的丢失或损坏都可能使得文件不再有价值。
在特定情况下,对于需要处理的数据进行完美重现是不必要的:一个近似的结果就足够了。通常,这些情况出现在多媒体应用中:超出人类听觉范围的声音不需要记录,人眼无法识别的颜色与梯度的细微之处也无需重现。
一个经典的示例是MPEG音频标准---通过去除高频声音相关的额外数据来降低音频文件的大小。这个标准的Layer-3规格允许多种去除数据的设定,这样渐进地从音频样本中去除更多的信息。
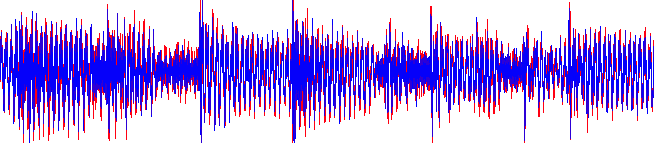
上图2中,两个波形叠加在一起:红色的为原来的歌曲波形,覆盖在其上的蓝色是经充分压缩的变体。展示的样本长度为1.5秒;作为原来波形文件的一部分,这段样本存储为160kB的数据。经压缩的变体,长度相同,但仅占用48kB的空间。
这是通过MPEG音频压缩算法得到的,调整歌曲的频率属性,去除超出人类听力范围(高至大约20kHz)的部分。这样,如上可见,并未显著地影响产生的波形,因此经压缩的声音不会明显地不同于原有的声音。
扔掉数据:视觉有损编码
正如声音文件的高频部分人耳无法辨别,图片也有高频部分:颜色的变化之处不足以人眼区分,或者由黑到白的渐变过程是如此的迅速导致无法看到渐变的部分。与声音处理一样,也可以从图片中去除这些高频部分;这就是JPEG图片格式的前提。
JPEG应用了MPEG音频所使用算法的一种变种,从包含于图片的频率部分抽取一个二维映射;该算法继而裁剪到这个频率部分,并重新合成图片。如下所示是这个过程的一个例子。

图3中,一张由4个16x16像素方块构成的图片,与该图片经JPEG编码后的图片进行比较。颜色或亮度上的尖锐变化被定义为高视觉频率的结果。这正是JPEG要去除的地方。结果,编码后图片的边缘比较模糊。4个方块的接触点特别模糊。
但JPEG的强大之处并不是编码具有尖锐变化边沿和角落的图片,而是低视觉频率的图片;照片就是其中的一个典型例子。

图4中,一张安塔利亚港的300x300图片,经过JPEG编码。原来的位图为270kB,经去除尖锐边缘和颜色变化,JPEG能够产生一张22kB的图片。对于人眼而言,图片的变化很小;即使像素有所改变,图片所展示的景色也完好无损。
这就是有损编码背后的主要概念:确切的数据并不重要,重要的是数据所呈现的信息。将JPEG算法用于编码软件程序是不明智的,但当数据表达了不必要的过多信息之时,有损编码就派上用场了。
感知冗余:视频编码
说到视频剪辑,通过结合无损和有损编码背后的原则,进一步压缩数据是有可能的。构建一个视频剪辑片段的最简单最幼稚的方法是合并连续的图片,作为视频帧来看待:MJPEG视频文件格式就是将一系列的JPEG图片看到独立的视频帧。
这种方法忽视了视频片段中固有的数据冗余:一个给定帧中包含的大多数信息同样会包含于其前一帧中。任何特定帧中仅有一小部分是新的信息;通过计算这部分信息所处的位置,然后仅存储这部分信息数据,那么就有可能大大地缩减视频帧的数据大小。

图5中,较之第一帧,视频的第二帧显示的变化非常小:仅仅航天飞机的排气羽流有显著的运动。事实上,发射塔后面的航天飞机固体助推器(SRB)(译注:见Wikipedia词条航天飞机固体助推器)和天空在两帧之间完全没有变化。那么就不用存储图片的这些部分,可能存储一个值:“没有变化”就可以了。
MPEG视频标准利用了这种内在的冗余作为算法的一部分。理论上,仅仅拍摄(a shot)的初始帧需要完整存储:拍摄的任何运动部分都可以作为与前一帧的相异之处来存储。初始帧,也称为一个内帧,存储为一张标准的JPEG图片,而后续的差异帧被称为间帧,或预测帧。
实际上,MPEG视频标准是以“流”来设计的,这样就能够从拍摄(a shot)的中间开始观看视频片段。但若仅提供视频的一个内帧(I-帧),那么预测帧(P-帧)是不可能插入它们的差异的。所以,通常会把I-帧每隔一定时间插入到视频片段中,而不管拍摄的场景(a shot)是否变化。
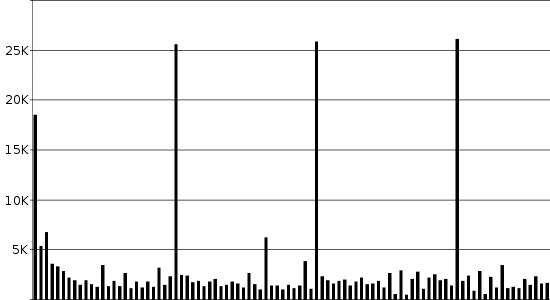
上图6中,视频片段每间隔25帧或一秒插入I-帧。后续的每个P-帧都比I-帧小得多,由于政治家在接受采访时一般都不会频繁移动,因此不同视频帧之间的不同之处更少。
图6使用的例子是一个4秒的400x224视频片段。以原始位图形式粗糙农户,生成文件的大小有26.7MB;通过结合使用有损编码和冗余的技术,MPEG视频标准能够将视频大小缩减到300kB,减小了99%。
总结:什么情况下可以有损编码
本文所列举的有损编码的例子都是应用于特殊情况的:音频,视频,图片。仅对于这些或者其他相关的东西,感知才是压缩过程中的一个重大因素。对于其他压缩目标,比如文档或软件程序,数据是什么样的就保存为什么样,非常重要。
人们一直在开发更加高级的特殊压缩方法,但数据压缩的多数常见实现都是基于本文讲述的技术:去除冗余和重复信息。当存在大量冗余数据时,数据压缩会表现得非常好,所以不要试图去压缩一个已经压缩过的文件。