标量量化入门（译）
简介
多数嵌入（embedding）模型会输出 $float32$ 数值精度的向量。这个精度虽然提供了信息高保真，但在真正重要的信息之外也带来一些资源浪费。对于给定的数据集，嵌入不可能在单个维度需要20亿种取值，特别是对于高维度向量而言（比如：386维及以上）。量化以一种有损的方式对向量进行编码，轻微降低信息保真而明显地降低存储空间占用。
理解标量量化的分桶
标量量化使用更小的数据类型对向量每一维的取值进行分桶。本文的余下部分将假设将 $float32$ 量化到 $int8$ 。为了准确地对值进行分桶，不能简单地将值四舍五入到最近的整数。许多模型输出向量的维度取值空间为 $[-1.0, 1.0]$，如果简单粗暴地四舍五入处理，那么 0.123 和 0.321 这两个不同的向量维度取值都会向下取整到 0。最终，一个向量仅会使用 $int8$ 可用 255 个桶中的2个桶，这样就丢失太多信息了。
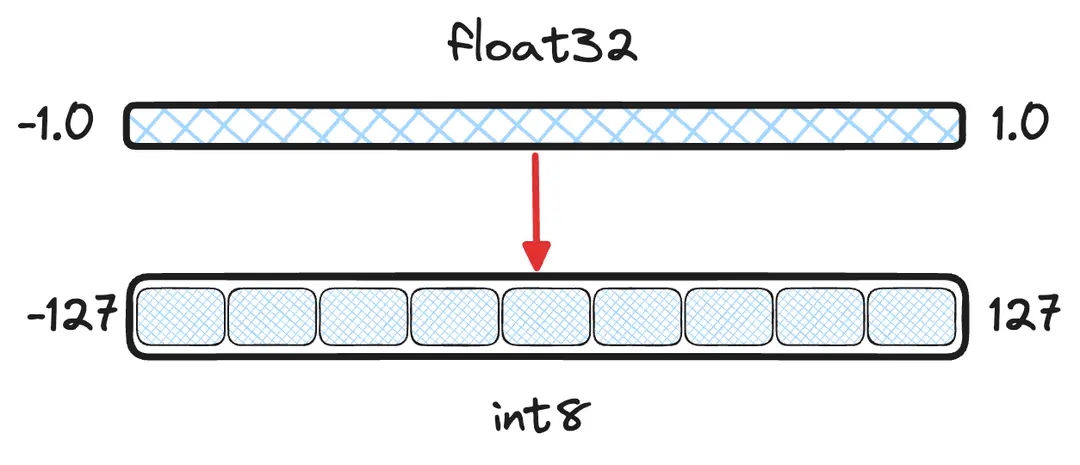
图1：量化目标图解 - 将 -1.0 到 1.0 之间的连续值分桶到离散的 $int8$ 数值。
这种数值转换背后的数学原理并不太复杂。我们可以先计算浮点数取值区间的最小和最大值，然后使用 最小-最大归一化) 对值进行线性变换（linearly shift）。
$$int8\approx \frac{127}{max-min} \ \times \left( float32-min \right)$$
$$float32\approx \frac{max-min}{127} \times int8+min$$
图2：$int8$ 和 $float32$ 之间的变换公式。注意：这两个变换是有损的，并不是精确变换。下面的例子中，仅使用 $int8$ 取值空间的正数部分。Lucene 的实现也是这样的。
标量量化的统计视角
分位点（quantile） 是指数值分布的一个切片，这个切片包含一定数量比例的值。例如：一种浮点数取值分布下 99% 的值落在 $[-0.75, 0.86]$ 这个分位点区间内，小于 $-0.75$ 和大于 $0.86$ 的值都被视为离群值/异常值（outliers），因此将 $-0.75$ 和 $0.86$ 分别视为实际的最小值和最大值。如果量化时将离群值包含在内，就意味着那些最常见的值可用的桶偏少了，可用桶少了也就意味着精度更差，信息损失更多。
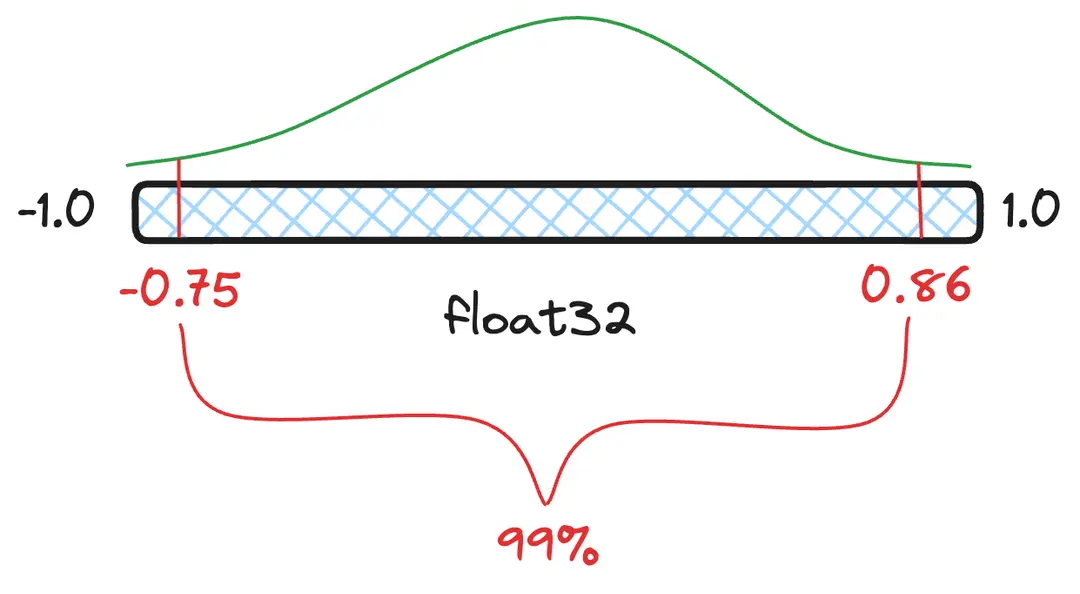
图3:图解 99% 置信区间(confidence interval)及对应的分位点数值，即 99% 的值落在 $[-0.75, 0.86]$ 这个范围内。
不错，我们现在知道如何对浮点值进行量化了，那么又应该如何计算两个量化后向量的距离呢？就像常规的点积计算一样简单吗？
标量量化的代数视角
目前为止仍然缺失关键的一块拼图 - 如何计算两个量化后向量之间的距离。本文并没有有意避开数学公式，下面也会出现更多数学内容。拿出你的铅笔，回忆一下多项式 和基础代数。
点积和余弦相似度的计算逻辑是将两个向量对应维度上的浮点值相乘，然后将所有维度上的结果相加。我们已经知道如何在 $float32$ 和 $int8$ 值之间做变换，那么应用变换后的乘法公式是什么样的呢？
$$float32_{i}\times float32_{i}^{\prime}\approx \left( \frac{max-min}{127} \times int8_{i}+min \right) \times \left( \frac{max-min}{127} \times int8_{i}^{\prime}+min \right)$$
将这个乘法公式展开后（为了简化，以 $\alpha$ 替代 $\frac{max-min}{127}$），如下所示：
$$\alpha^{2} \times int8_{i}\times int8_{i}^{\prime}+\alpha \times int8_{i}\times min+\alpha \times int8_{i}^{\prime}\times min+min^{2}$$
接下来就更有意思了 - 这个算式中仅有一个部分要求同时提供两个变量值。然而，点积并不只是两个浮点数相乘，而是两个向量的每一维对应的浮点值相乘。假设向量的维度为 $dim$，那么以下部分算式都可以提前计算好存下来。
$dim\times \alpha^{2}$ 即 $dim\times \left( \frac{max-min}{127} \right)^{2}$ ，可以提前计算好存为单个浮点数。
$\sum_{i=0}^{dim-1} min\times \alpha \times int8_{i}$ 和 $\sum_{i=0}^{dim-1} min\times \alpha \times int8_{i}^{\prime}$ 都可以分别提前计算好存为单个浮点数，或者在检索时计算一次。
$dim\times min^{2}$ 也可以提前计算好存为单个浮点数。
那么：
$$dim\times \alpha^{2} \times dotProduct\left( int8,int8^{\prime} \right) +\sum_{i=0}^{dim-1} min\times \alpha \times int8_{i}+\sum_{i=0}^{dim-1} min\times \alpha \times int8_{i}^{\prime}+dim\times min^{2}$$
点积的整个算式中仅 $dotProduct\left( int8,int8^{\prime} \right)$ 部分需要在检索时计算，加上其他提前计算好的部分就能得到结果。
量化的精度保证
那么，这样量化计算的准确性如何？量化后损失信息没有？是的，损失了一些信息，不过量化正是基于我们事实上并不需要所有信息的假设。对于训练得到的嵌入模型，向量各个维度的值分布通常不存在厚尾性(fat-tails)。这意味着值分布存在一定的局部性和一致性。此外，量化对每一维度引入的误差是相互独立的，这意味着对于向量的典型运算（比如点积），误差一定程序上会抵消。
总结
哟，一写就写了一堆内容。现在你应该很好地理解了量化的技术优势，其背后的数学原理，以及如何将线性变换考虑在内计算向量之间的距离。