2013-网易-校园招聘-C++开发工程师
Fibonacci number
F(n)的值是多少?
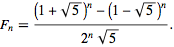
常规算法:根据Fabonacci的定义,递归求值。时间复杂度$ O(2^n) $
def fibobacci(n):
return n>=2 and fibonacci(n-2) + fibonacci(n-1) or n
迭代:利用循环取代递归。时间复杂度O(n)
def fibonacci(n):
a, b = 0, 1
for i in range(n):
a, b = b, a+b
return a
迭代算法的变种 :利用python的generator,原理一样,只是应用场合不一样。
def fibonacci():
a, b = 0, 1
while 1:
yield a
a, b = b, a+b
f = fibonacci()
n = 100
for i in range(n+1):
print(next(f)
利用矩阵运算来加速的算法:(还没懂)算法复杂度$ O(\log n) $
import numpy
fibonacci_matrix = numpy.matrix([1,1],[1,0], dtype=numpy.ndarray)
def fibonacci(n):
return fibonacci_matrix**(n-1)[0, 0]
数学方法:使用Fibonacci序列的通用公式:
from math import sqrt
def fibonacci(n):
return int(((1+sqrt(5))/2)**n/sqrt(5))
虽然数学方法在4种方法中速度最快,但当n越大,其计算精度偏差越大。
图的遍历
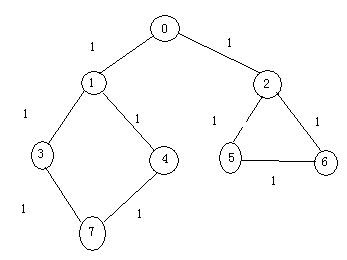
大文件处理
设计算法从文件中随机取K行(内存够存储K行),每行被取的概率相等,算法复杂度要低。(具体的记不太清楚了)
CAS(Compare And Swap)
bool compare_and_swap(int *accum, int *dest, int newval)
{
if(*accum == *dest)
{
*dest = newval;
return true;
}
return false;
}
CAS方式实现的进队列操作:
EnQueue(x) //进队列
{
q = new record();
q->value = x;
q->next = NULL;
do {
p = tail; //取链表尾指针的快照
}while(CAS(p->next, NULL, q) != TRUE) //如果没有把结点链上,再试
CAS(tail, p, q); //置尾结点
}
排序算法
不稳定排序算法可能会在相等的键值中改变记录的相对次序,但是稳定排序算法从来不会如此。
稳定的
-
冒泡排序(Bubble sort) --- $ O(n^2) $
-
插入排序(Insertion sort) --- $ O(n^2) $
-
桶排序(Bucket sort) --- $ O(n) $,需要$O(k)$额外空间
-
计数排序(Counting sort) --- $ O(n+k) $,需要$O(n+k)$额外空间
-
归并排序(Merge sort) --- $ O(n \log n) $,需要$O(n)$额外空间
-
基数排序(Radix sort) --- $ O(n \times k) $,需要$O(n)$额外空间
不稳定的
-
选择排序(Selection sort) --- $ O(n^2) $
-
希尔排序(Shell sort) --- $ O(n \log n) $
-
堆排序(Heap sort) --- $ O(n \log n) $
-
快速排序(Quick sort) --- $ O(n \log n) $
代码实现
冒泡排序---Python:
def bubbleSort(L):
print 'start bubble sort:'
print L
count = 0
while True:
step = 0
for i in range(len(L)-1):
if L[i] > L[i+1]:
L[i], L[i+1] = L[i+1], L[i]
print L
step += 1
count += 1
if step == 0:
return L, 'totalstep:', count
计数排序---C:
#include <stdlib.h>
void counting_sort(int *array, int size)
{
int i, min, max;
min = max = array[0];
for(i=1; i<size; i++)
{
if(array[i] < min)
min = array[i];
else if(array[i] > max)
max = array[i];
}
int range = max-min+1;
int *count = (int *)malloc(range * sizeof(int));
for(i = 0; i < range; i++)
count[i] = 0;
for(i = 0; i < size; i++)
count[array[i]-min]++;
int j, z = 0;
for(i=min; i<=max; i++)
for(j=0; j<count[i-min]; j++)
array[z++] = i;
free(count);
}
快速排序---Python:
def qsort(L):
if not L: return []
return qsort([x for x in L[1:] if x < L[0]]) + L[0:1] + \
qsort([x for x in L[1:] if x>=L[0]])
2013-小米科技-校园招聘-笔试-软件开发工程师
完全二叉树
深度为k的,有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时,称之为完全二叉树 。
这种树的特点是:1.叶子结点只可能在层次最大的两层上出现; 2.对任一结点,若其右分支下的子孙的最大层次为l,则其左分支下的子孙的最大层次必为l或l+1。
具有n个结点的完全二叉树的深度为$ [\log n]+1 $
指针的基本理解
已知int* p = &n,请问*p是什么?
*p是n的值
理解指针 :
-
每个指针都对应一个类型。这个类型表明指针指向哪一类对象。特殊的void* 类型代表通用指针。比如说,malloc函数返回一个通用指针,然后通过显式强制类型转换或者赋值操作那样的隐式强制类型转换,将它转换成一个有类型的指针。
-
每个指针都有一个值。特殊的NULL(0)值表示该指针没有指向任何地方。
-
指针用&运算符创建。(注:因为leal指令是设计用来计算存储器引用的地址的,&运算符的机器代码实现常常用这条指令来计算表达式的值)
-
数组与指针紧密联系。一个数组的名字可以像一个指针变量一样使用(但是不能修改)
-
将指针从一个类型强制转换成另一种类型,只改变它的类型,而不改变它的值。强制类型转换的一个效果是改变指针运算的伸缩。例如,如果p是一个char*类型的指针,它的值是P,那么表达式(int*)p+7计算为P+28,而(int*)(p+7)计算为P+7。(回想一下,强制类型转换的优先级高于加法)
-
指针也可以指向函数。例如,如果我们有一个函数,用下面的这个原型定义:
int fun(int x, int *p)
然后,我们可以声明一个指针fp,将它赋值为这个函数,代码如下:
(int) (*fp)(int, int *);
fp = fun;
然后用以下指针来调用这个函数:
int y = 1;
int result = fp(3, &y);
函数指针的值是该函数机器代码表示中第一条指令的地址。
93&-8等于多少
11011101 & 11111000 = 11011000 = 88
已知(he)^2 = she,请求出s, h, e各自的值为多少?
s = 6; h = 2; e = 5;
给定二维数组a[1...100][1...65],以行序进行存储,假设数组的基地址为10000,每个元素需要2个存储单元,请求出元素a[56][21]的存储地址。
$$ (55 \times 65 + 22) \times 2 + 10000 = 17194 $$
给定一个数组a,求数组result,其中result[i]的值为除a[i]之外的其他a的元素值的乘积(假设不会溢出)。算法的时间,空间复杂度要尽可能低。
int* getProduct(int* a, int n)
{
int allproduct = 1;
int index;
for(index=0; index<n; index++)
allproduct *= a[index];
int* productResult = new int[n];
for(index=0; index<n; index++)
productResult[index] = allproduct / a[index];
return productResult;
}
时间复杂度为O(n)
int* getProduct(int* a, int n)
{
int* productResult = new int[n];
int i, j, temp;
for(i=0; i<n; i++)
{
temp = 1;
for(j=0; j<n; j++)
{
if(j != i)
temp *= a[j];
}
productResult[i] = temp;
}
return productResult;
}
时间复杂度为O(n^2)
给定一个数组a,其中有3个元素出现了两次,其余元素仅出现一次。请找出其中仅出现一次的任意一个元素。算法的时间,空间复杂度要低
方法一:先排序,然后对元素依次两两比较遍历一遍排好序的数组,如果两个元素不同,则输出第一个元素,并退出循环。如果相同,则跳过下一个元素,再次开始两两比较。
方法二:先找出数组a中的最大元素x,创建一个大小为x的数组temp,并所有元素初始化为-1。遍历数组a,temp[a[i]]++。再遍历temp,如果temp[i]==0,则返回i,并退出循环。
给定n个人,以及m对人之间的关联(以二维数组的方式存储),人与人之间直接关联或间接关联形成一个朋友圈。请找出给定信息的朋友圈的个数。算法时间空间复杂度要低。并分析其时间空间复杂度。
使用 合并-查找算法 (并查集)
连通问题的快速查找算法:算法的基础是一个整型数组,当且仅当第p个元素和第q个元素相等时,p和q是连通的。初始时,数组中的第i个元素的值为i,$0 \le i < N$。为实现p与q的合并操作,我们遍历数组,把所有名为p的元素值改为q。我们也可以选择另一种方式,把所有名为q的元素改为p。
2013-腾讯-校园招聘-笔试-后台开发工程师
黑盒,白盒测试的目的
TCP三次握手包含的指令(SYN, ACK)
完全二叉树的结点数为769,求其叶子结点数目
(769-x)*2 = 769-1 => x=385
C++的四种类型转换符
快速排序
有一个指针void *mPem指向一段分配好的内存空间,现在创建类A的对象a,如何使得a在其上申请内存空间?
难道真是A* a = (A*)mPem么?
虚继承与多态
#include <stdio.h>
#include<stdlib.h>
using namespace std;
class A{
public:
A():a(0){}
void S(){
printf("aaa%d",0);
}
int a;
};
class B:public A
{
public:
B():a(2){}
void S(){
printf("bbb%d",1);
}
int a;
};
int main()
{
A *a = new B();
a->S();
printf("%d",a->a);
}
BITMAP的简单实现:使用char类型数组
char* a;
...
void set(int n) //设置第n位为1
{
int index = (n-1)/8;
a[index] |= 1<<(n-1-(n-1)%8)
}
矩阵向右旋转90度的实现
int maxtrix[M][N];
...
int reverseMatrix[N][M];
int i, j;
for(i=0; i<M; i++)
{
for(j=0; j<N; j++)
{
reverseMatrix[j][M-1-i] = matrix[i][j];
}
}
数据结构:线性结构与非线性结构
综合考虑等待时间和执行时间的进程调度算法?
高响应比优先调度算法
无法提高可靠性的RAID是?
RAID0
类型的空间占用
下列哪个占用的空间最大?
A.1 B.'1' C."1" D.1.0
答:D
union和struct结构的存储与空间占用问题(对齐)
1.
联合提供了一种方式,能够规避C语言的类型系统,允许以多种类型来引用一个对象。
union U3 {
char c;
int i[2];
double v;
}
对于类型union U3*的指针p, p->c、p->i[0]和p->v引用的都是数据结构的起始位置。一个联合的总的大小等于它最大字段的大小。
2.
许多计算机系统对基本数据类型合法地址做出了一些限制,要求某种类型对象的地址必须是某个值K(通常是2, 4和8)的倍数。这种对齐限制简化了形成处理器和存储器系统之间接口的硬件设计。例如,假设一个处理器总是从存储器中取出8个字节,则地址必须是为8的倍数。如果我们能保证将所有的double类型数据的地址对齐成8的倍数,那么就可以用一个存储器操作来读或者写值了。否则,我们可能需要执行两次存储器访问,因为对象可能被分放在两个8字节存储器块中。
无论数据是否对齐,IA32已经都能正确工作。不过,Intel还是建议要对齐数据以提高存储器系统的性能。Linux沿用的对齐策略是,2字节数据类型(例如short)的地址必须是2的倍数,而较大的数据类型(例如int、int*、float和double)的地址必须是4的倍数。
二叉树中序遍历
最小堆(堆排序)
堆排序(Heap Sort)只需要一个记录大小的辅助空间,每个待排序的记录仅占有一个存储空间。
堆的定义如下:n个元素的序列{K1, K2,...,Kn}当且仅当满足关系时,称之为堆: Ki <= K2i 并且 Ki <= K2i+1 或 Ki >= K2i 并且 Ki >= K2i+1
若将和此序列对应的一维数组看成是一个完全二叉树,则堆的含义表明,完全二叉树中所有非终端结点的值均不大于(或不小于)其左、右孩子结点的值。由此,若序列{Ki,K2,...,Kn}是堆,则堆顶元素(或完全二叉树的根)必为序列中n个元素的最小值(或最大值)。
若在输出堆顶的最小值之后,使得剩余n-1个元素的序列重又建成一个堆,则得到n个元素中次小值。如此反复执行,便能得到一个有序序列,这个过程称之为堆排序。
由此,实现堆排序需要解决两个问题:(1)如何由一个无序序列建成一个堆?(2)如何在输出栈顶元素之后,调整剩余元素成为一个新的堆?
一个线段上,任取两点,截成三段,能组成三角形的概率
1/4 (怎么算?)
思考1:线段等分成两个区间。两点属于同一区间的概率是1/2,属于不同区间且两点距离大于等于线段长度一半的概率是1/2 * 1/2,则1-1/2-1/4 = 1/4;
思考2:线性规划。百度知道
哈希表
哈希函数的构造方法
-
直接定址法:取关键字或关键字的某个线性函数值为哈希地址
-
数字分析法:假设关键字是以r为基的数(如:以10为基的十进制数),并且哈希表中可能出现的关键字都是事先知道的,则可取关键字的若干数位组成哈希地址。
-
平方取中法:取关键字平方后的中间几位为哈希地址
-
折叠法:将关键字分割成位数相同的几部分(最后一部分的位数可以不同),然后取这几部分的叠加和(舍去进位)作为哈希地址,这方法称为折叠法。
-
除留余数法:取关键字被某个不大于哈希表表长m的数p除后所得余数为哈希地址。
-
随机数法:选择一个随机函数,取关键字的随机函数值为它的哈希地址,即H(key)=random(key),其中random为随机函数
实际工作中需视不同的情况采用不同的哈希函数。通常,考虑的因素有:
-
计算哈希函数所需时间(包括硬件指令的因素)
-
关键字的长度
-
哈希表的大小
-
关键字的分布情况
-
记录的查找频率
处理冲突的方法:
-
开放定址法
-
再哈希法
-
链地址法
-
建立一个公共溢出区
程序员面试宝典
用一个表达式,判断一个数X是否是2的N次方(2,4,8,16,...),不可用循环语句。
下面程序的结果是多少?
#include <iostream>
#include <string>
using namespace std;
int main()
{
int count = 0;
int m = 9999;
while(m){
count++;
m=m&(m-1);
}
cout << count << endl;
return 0;
}
There are two int variables: a and b, don't use "if", "?:", "switch" or other judgement statements, find out the biggest one of the two numbers.
int max = ((a+b)+abs(a-b)) / 2;
如何将a, b的值进行交换,并且不使用任何中间变量?
简而言之,用异或语句比较容易,不用担心超界的问题。
如果采用:
a=a+b;
b=a-b;
a=a-b;
这样做的缺点就是如果a, b都是比较大的两个数,a=a+b时就会超界。
而采用:
a=a^b;
b=a^b;
a=a^b;
无需担心超界的问题,这样就比较好